11002. Покраска дерева
Вам задано дерево
(неориентированный связный ацикличный граф), состоящее из n вершин. Вы
играете в игру на этом дереве.
Изначально все вершины белые. На
первом ходу игры Вы выбираете одну вершину и красите ее в черный. Затем на
каждом ходу Вы выбираете белую вершину, смежную (соединенную ребром) с любой
черной вершиной и красите ее в черный.
Каждый раз, когда вы выбираете
вершину (даже во время первого хода), Вы получаете количество очков, равное
размеру компоненты связности, состоящей только из белых вершин, содержащей
выбранную вершину. Игра заканчивается, когда все вершины покрашены в черный
цвет.
Рассмотрим следующий пример:
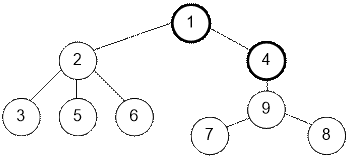
Вершины 1 и 4 уже
покрашены в черный цвет. Если выберете вершину 2, то
получите 4 очка за компоненту связности, состоящую из
вершин 2, 3, 5 и 6. Если выберете вершину 9, то
получите 3 очка за компоненту связности, состоящую из
вершин 7, 8 и 9.
Ваша задача – максимизировать количество
очков, которое Вы получите.
Вход. Первая строка содержит одно
целое число n (2 ≤ n ≤ 2 * 105) –
количество вершин в дереве.
Каждая из следующих n – 1 строк
описывает ребро дерева. Ребро i описывается двумя целыми числами ui
и vi (1 ≤ ui, vi ≤
n, ui ≠ vi), номерами вершин,
которые оно соединяет.
Гарантируется, что заданные ребра
образуют дерево.
Выход. Выведите одно целое число – максимальное
количество очков, которое вы получите, если будете играть оптимально.
|
Пример
входа 1 |
Пример
выхода 1 |
|
9 1 2 2 3 2 5 2 6 1 4 4 9 9 7 9 8 |
36 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
5 1 2 1 3 2 4 2 5 |
14 |
РЕШЕНИЕ
дерево
Анализ алгоритма
Количество полученных очков однозначно определяется первой
выбранной вершиной. Остается перебрать в качестве первой все возможные вершины,
вычислить полученное количество очков и вывести максимальное среди них значение.
Запустим поиск в глубину из
вершины 1. Вычислим weight[v]
– размер поддерева (количество
вершин) с корнем в вершине v. Пусть to1, to2, …, tok – сыновья v. Тогда
weight[v] = 1 + weight[to1] + weight[to2] + … + weight[tok]
Второй поиск в глубину будет
проходить по всем вершинам и пересчитывать максимальное количество очков,
которое можно получить если стартовать из этой вершины.
Рассмотрим
функцию dfs2. Мы находимся в вершине v, предком которой является p. Если первым ходом игры выбрать вершину v, то количество
полученных очков составляет s.
void dfs2(int v, int p, long long s)
Сделаем переход по ребру (v, to) и покажем как вычислить ответ,
если игру изначально стартовать из вершины to. Фактически произведем переподвешивание дерева с вершины v в вершину to.
Слева приведено дерево с корнем в
v. Вершина to – один из ее сыновей, p – предок. Справа приведено дерево с корнем
в to.
Для вычисления weight[to] правого дерева необходимо из
значения s в левом дереве вычесть weight[to] левого дерева и прибавить количество вершин в области,
обозначенной пунктиром. Оно равно n – weight[to].
Пример
Пусть первой выбранной вершиной будет 1. Тогда количество
полученных очков составит 25.
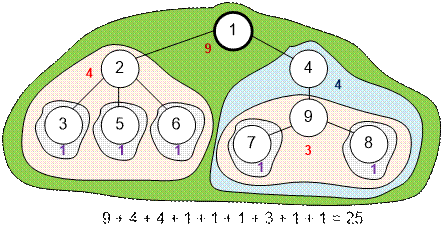
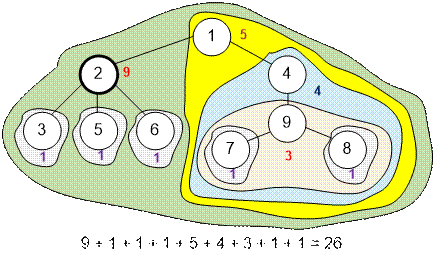
Если первой выбранной вершиной будет 2, то количество
полученных очков равно 26. Переход от вершины 1 к вершине 2 произведем
следующим образом. Вычтем из s = 25 значение weight[2] = 4 и прибавим (9 –
weight[4]) = 5. Получим 25 – 4 + 5 = 26, значение s для дерева с корнем в вершине 2.
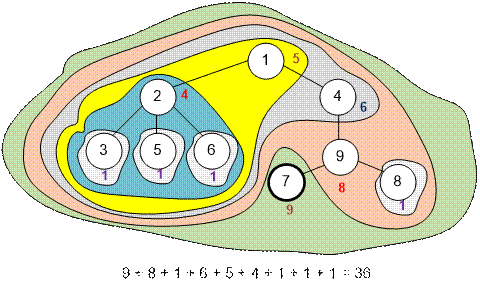
Максимальное количество очков – 36, будет получено если
начать игру с вершины номер 7.
Реализация алгоритма
Объявим список смежности графа g.
vector<vector<int>>
g;
vector<int> weight;
Функция dfs1
запускает поиск в
глубину из вершины v, предком которой является p. Вычисляем weight[v] – размер поддерева (количество
вершин) с корнем в вершине v.
void dfs1(int v, int p)
{
weight[v] = 1;
for (int to : g[v])
if (to != p)
{
dfs1(to, v);
weight[v] += weight[to];
}
}
Функция
dfs2 запускает поиск в глубину из вершины v, предком которой является p. Если
первым ходом игры выбрать вершину v, то количество полученных очков составит
s.
void dfs2(int v, int p, long long s)
{
res = max(res, s);
for (int to : g[v])
if (to != p) dfs2(to, v, s - weight[to] + n - weight[to]);
}
Основная
часть программы. Читаем входные данные. Строим граф.
scanf("%d", &n);
g.resize(n
+ 1);
weight.resize(n
+ 1);
for (i = 1; i < n; i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}
Запускаем
поиск в глубину из вершины 1.
dfs1(1, 0);
В
переменной s вычислим сумму всех чисел в
массиве weight. Оно равно количеству полученных очков
в случае, если первой в игре выбрать вершину номер 1.
s = 0;
for (i = 1; i <= n; i++)
s += weight[i];
Запускаем
второй поиск в глубину из вершины 1.
dfs2(1, 0,
s);
Выводим
ответ.
printf("%lld\n", res);
